ƒƒ“ƒY ƒXƒ|[ƒeƒB[ ”¯Œ^ 593166-E^x-y can be written as
Normal Equations 1The result of this maximization step are called the normal equations b 0 and b 1 are called point estimators of 0 and 1 respectively X Y i = nb 0 b 1 X X i X X iY i = b 0 X X i b 1 X X2 2This is a system of two equations and two unknownsQED Definition An element y in B is called a complement of an element x in B if xy=1 and xy=0 Theorem 2 For every element x in B, the complement of x exists and is unique Proof Existence Let x be in B x' exists because ' is a unary operation X' is a complement of xE−λ = λ X∞ k=0 λk k!
What Does It Mean To Reflect Over The Y X Line Quora
E^x-y can be written as
E^x-y can be written as-2 0 ≤ X ≤ 1 EY X = X − 1 2 1 < X ≤ 2 (b) Let g(x) be the estimate from part (a) Find Eg(X) and var(g(X)) g(X) is a derived random variable that is defined as g(X) = 1 2, 0 ≤Y 2 − e x y − e x = 0 This is a second degree polynomial in y;
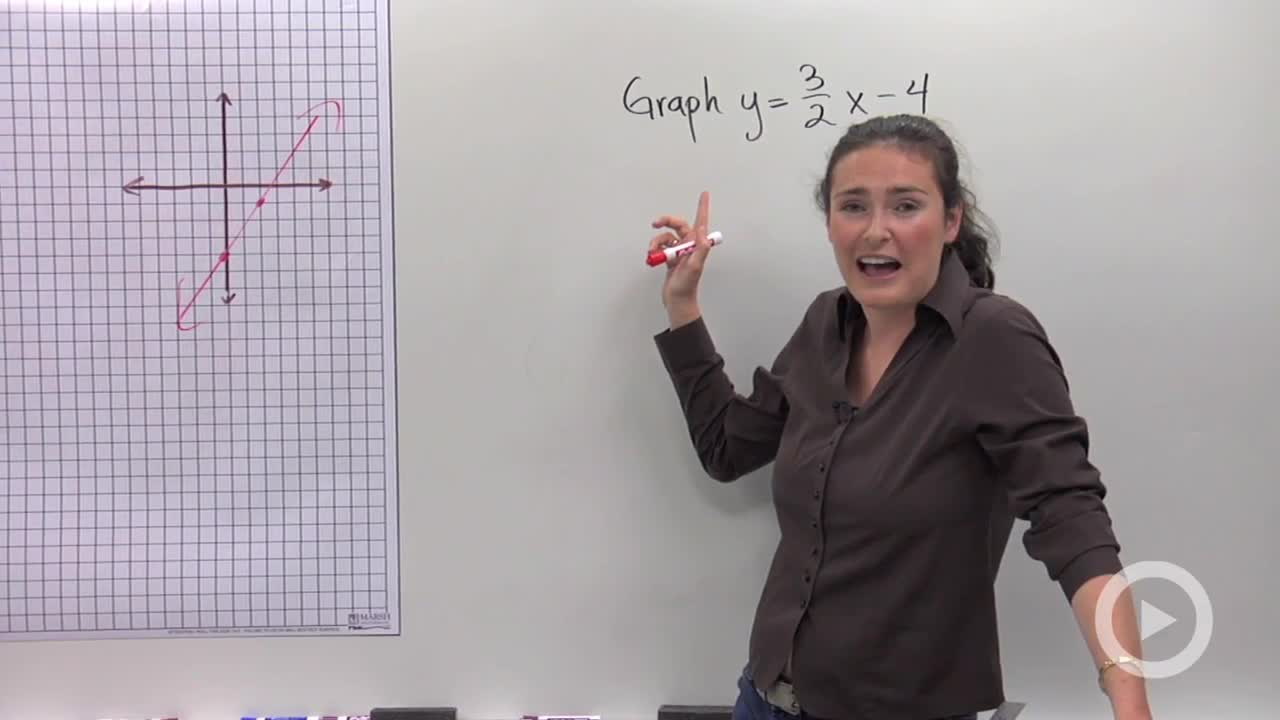



How To Graph A Line Using Y Mx B Problem 1 Algebra Video By Brightstorm
Var b k Var y k k Cov y y xx Cov y y y y s s s s The variance of b0 is 2 Var b Var() ()2 (,)011 y xVarb xCovy b First, we find that 111 1 01 1 (,) () 1 ()( ) 1 0000 0 ii i ii iiii i ii i i i Cov y b E y E y b E b Ecy Eccxc n n So 2 2 0 1 xx x Var b ns Covariance The covariance between b0 and b1 is 01 1 1 2 (,) (,) () xx Cov b b Cov y bIntegrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Y 1(x) = e3x and y 2(x) = e−2x These are linearly independent and therefore the general solution is y cf(x) = Ae3x Be−2x The equation k2 −k −6 = 0 for determining k is called the auxiliary equation Task By substituting y = ekx, find values of k so that y is a solution of d2y dx2 −3 dy dx 2y = 0
Answer (1 of 3) First, I request you to kindly read the chapter on Expectation from any basic book on Statistics There you will find the following (i) If X is a random variable taking the values x_i ( i=1,2,3,n) with corresponding probabilities as p_i(i=1,2,3,n) then Expectation of x isIt is also, of course, a function ofClick here👆to get an answer to your question ️ If x^y = e^x y , then dydx is equal to Join / Login >> Class 12 >> Maths >> Continuity and Differentiability >> Derivatives of Implicit Functions If x y y x = a b then find that d x d y
Proof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ NX and Y, ie corr(X,Y) = 1 ⇐⇒ Y = aX b for some constants a and b The correlation is 0 if X and Y are independent, but a correlation of 0 does not imply that X and Y are independent 33 Conditional Expectation and Conditional Variance Throughout this section, we will assume for simplicity that X and YLet X and Y be two discrete random variables Then E (aX bY) = aE (X)bE (Y) for any constants a,b ∈ R Note No independence is required Proof E (aX bY) = P x,y (axby)p(x,y) = a P x,y xp(x,y)b P x,y yp(x,y) P x p(x,y) = p(y) x = a P x xp(x)b P y yp(y) = aE (X)bE (Y) Example Binomial distribution Let X ∼ Bin(n,θ) Then X = X 1



Graphing Equations And Inequalities Slope And Y Intercept In Depth




If X A B C D And Y F B D G Find I X Y Video
7b E(a ± X) * b = (a ± E(X)) * b 8 E(X Y) = E(X) E(Y) (The expectation of a sum = the sum of the expectations This rule extends as you would expect it to when there are more than 2 random variables, eg E(X Y Z) = E(X) E(Y) E(Z)) 9 If X and Y are independent, E(XY) = E(X)E(Y)The nature of the underlying relation is Y = a e b x, where alpha and beta are parameters of the relation To get this relation in linear model form, one transforms both sides of the equation to obtain ln(Y) = ln(a e b x) = ln(a) ln(e b x) = ln(a) b x = b 0 b 1 x In linearized form b 0 = ln(a) and b 1 = bE(aX bY c) = aE(X)bE(Y)c for any a,b,c ∈ R 1 Let's use these definitions and rules to calculate the expectations of the following random variables if they exist Example 1 1 Bernoulli random variable 2 Binomial random variable 3 Poisson random variable 4 Negative binomial random variable
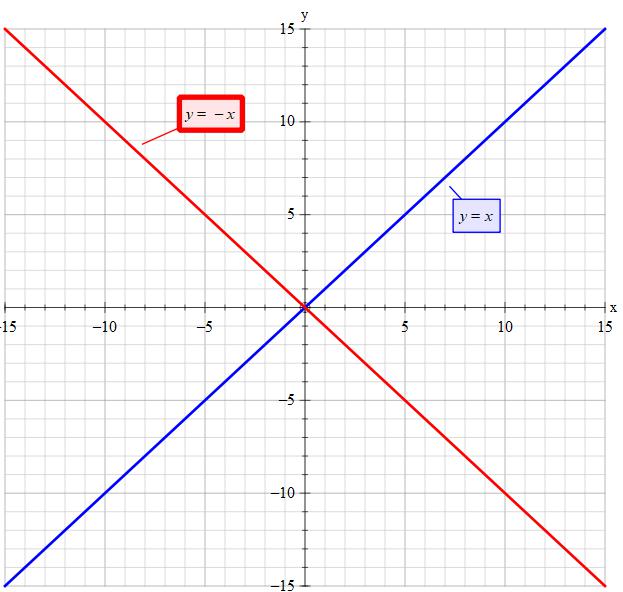



What Is The Basic Difference Between The Lines Y X And Y X Socratic




If A X B Y C Z And B 2 Ac Then Show That Y 2zx Z X Cbseassistance
(b) P(Y 3) = F(3) = R 3 2 x 6 dx= x 2 12 i x=3 x=2 = 3 12 2 12 = 5 12 requires (i) summation (ii) integration and is a value of a (i) probability density function (ii) cumulative distribution function which is a (i) stepwise (ii) smooth increasing function (c) E(Y) = (i) P yf(y) (ii) R yf(y)dy (d) Var(Y) = (i) E(X2) 2 (ii) E(Y2) 2 (e) M(t(b 0;b 1) E (Y (b 0 b 1X))2 (5) This is a function of the complete distribution, so we can't get it from data, but we can approximate it with data The insample, empirical or training MSE is MSE\(b 0;b 1) 1 n i=1 (y i (b 0 b 1x i)) 2 (6) Notice that this is a function of b 0 and b 1;Expected Value and Standard Dev Expected Value of a random variable is the mean of its probability distribution If P(X=x1)=p1, P(X=x2)=p2, n P(X=xn)=pn E(X) =
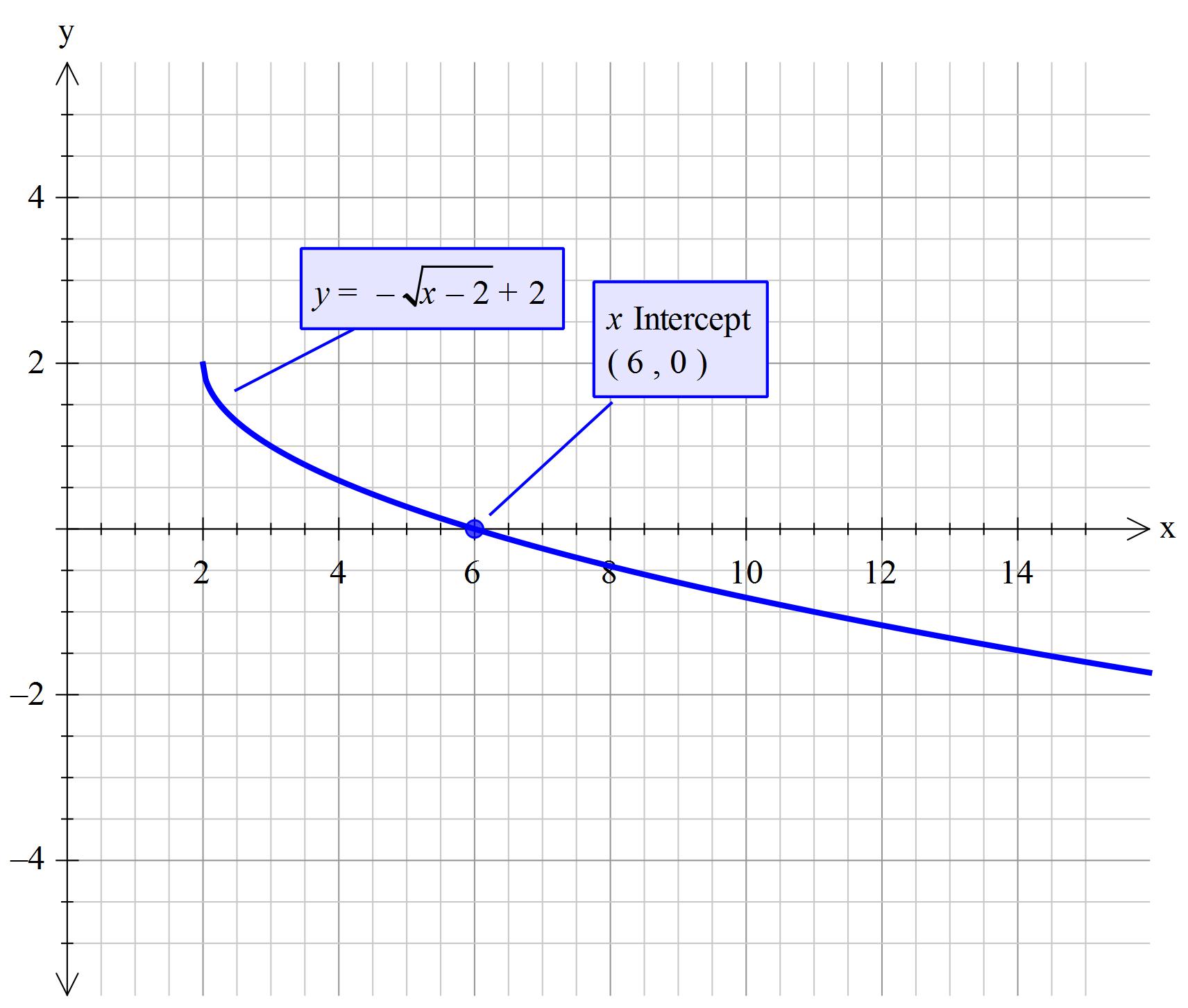



How Do You Graph Y Sqrt X 2 2 Socratic



What Does It Mean To Reflect Over The Y X Line Quora
Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USGraph y=e^ (x) y = e−x y = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0E(x,t) = E max cos(kx ωt φ), B(x,t) = B max cos(kx ωt φ) E is the electric field vector, and B is the magnetic field vector of the EM wave For electromagnetic waves E and B are always perpendicular to each other and perpendicular to the direction of propagation The direction of propagation is the direction of E x B Let the fingers of your right hand point in the direction of E
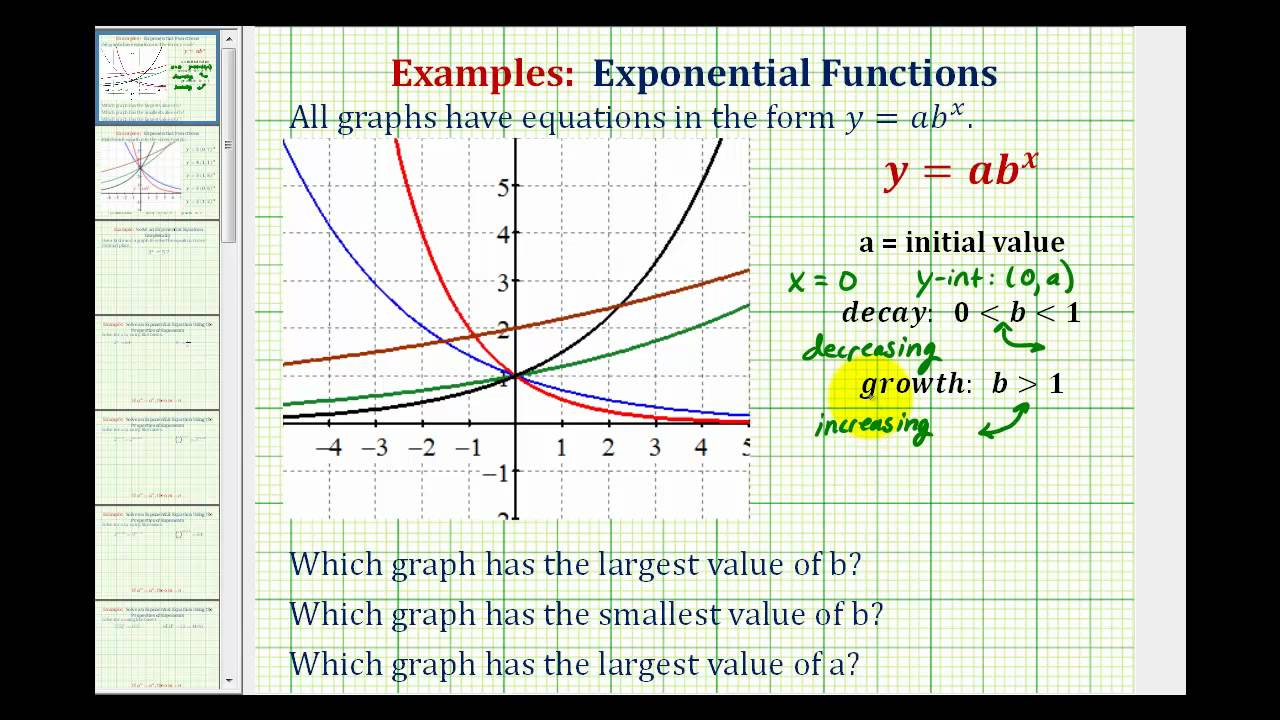



Ex Determine Exponential Graphs That Have Specific Characteristics Y Ab X Youtube
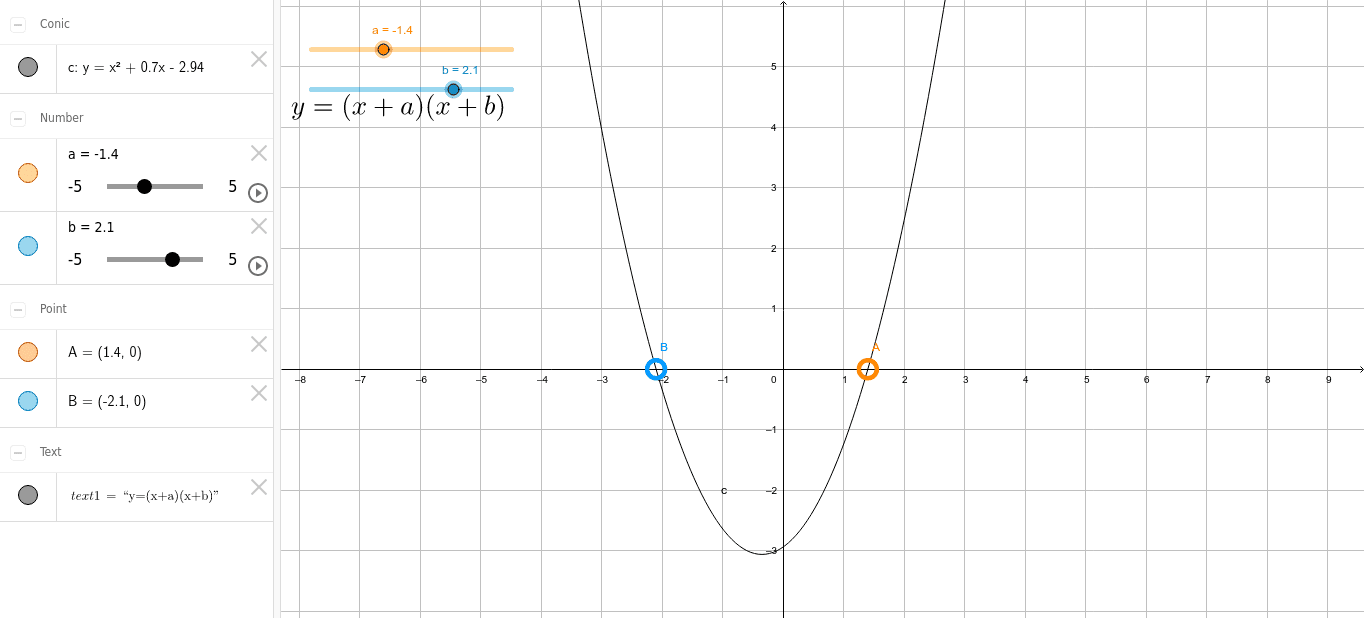



Y X X X B Geogebra
Integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;The fitted regression line/model is Yˆ = X For any new subject/individual withX, its prediction of E(Y)is Yˆ = b0 b1X For the above data, • If X = −3, then we predict Yˆ = − • If X = 3, then we predict Yˆ = • If X =05, then we predict Yˆ = 2 Properties of Least squares estimators It is usually best to see how we use these two facts to find a potential function in an example or two Example 2 Determine if the following vector fields are conservative and find a potential function for the vector field if it is conservative →F = (2x3y4 x)→i (2x4y3 y)→j F → = ( 2 x 3 y 4 x) i → ( 2 x 4 y 3 y) j →




Linear Function Calculus Wikipedia




A Comprehensive Guide To Logarithmic Regression By Pratik Shukla Heartbeat
E−λ = λ The easiest way to get the variance is to first calculate EX(X −1), because this will let us useB r(x) = fy2X d(x;y) 0 and center x2Xas the set of points whose distance from xis less than or equal to r, B r(x) = fy2X d(x;y) rg The term \ball" is used to denote a \solid ball," rather than the \sphere" of points whose distance from the center xis equal to r Example 1311Let us check directly that E is a base for a topology Suppose that x,y∈X and ε,δ>0If z∈B(x,δ)∩B(y,ε),then B(z,α) ⊂B(x,δ)∩B(y,ε) (102) where α=min{δ−d(x,z),ε−d(y,z)},see Figure 102 This is a formal consequence of the triangle inequality For example let us show that B(z,α) ⊂




A X B Y M B X A Y N Solve This Equation Mathematics Topperlearning Com 0fu87vuu
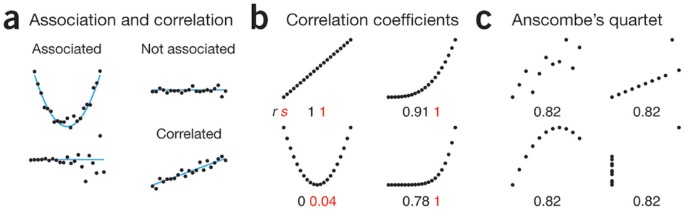



Association Correlation And Causation Nature Methods
In this case if b or x is 0 then, e^0 = 1 So at the yintercept or x = 0, the function becomes y = a * 1 or y = a Therefore, the constant a is the yintercept of the curve The other parameter in our equation is b If b is very small and greater than 0, the function flattens out The curve increases at a slower rate then for large b'sDrones asteroids Aerial Analysis – Challenge 1 Some humans see a photo as an image that perhaps captures a moment in time To thinking men, it can be carefully read to see what has happened in the past and perhaps what might occur in the futureOr E {\displaystyle \mathbb {E} } The expected value is also known as the expectation, mathematical expectation, mean, average, or first moment Expected value is a key concept in economics, finance, and many other subjects By definition, the expected value of a constant random variable X = c {\displaystyle X=c}



Quadratics




Exponential Function Wikipedia
63 Expected value If X and Y are jointly continuously random variables, then the mean of X is still given by EX = Z ∞ −∞ xfX(x)dx If we write the marginal fX(x) in terms of the joint density, then this becomes EX =S T D A U F E E L V W N X M Y Z A B K C U D B E L I E V E F Word search puzzle words to find S E E H E A R R E A D F E E L T A L K H O P E K N O W T H I N K G U E S S D R E A M B E L I E V E U N D E R S T A N D Reprinted with permission by the Dana Alliance for Brain Initiatives "FORMING WORDS" This puzzle gives you five key words toNOTES ON METRIC SPACES JUAN PABLO XANDRI 1 Introduction Let X be an arbitrary set, which could consist of vectors in Rn, functions, sequences, matrices, etc We want to endow this set with a metric;



Exponential Functions




Excel Formula Sum If Equal To Either X Or Y Exceljet
Answer (1 of 2) Conditional expectation is difficult to work with in the most general case Here is a link to the proof in the general case, but it may not be that informative if you are not familiar with measure theory Law of total expectation I will give you a "proof" in the special case4 the identity matrix Hence, I = C = g(t) = e(AB)te Bte At for all t After multiplying by eAteBt on both sides we have eAteBt = e(AB)t Exercises 1 If = 0, the zero matrix, prove that eA = I A 2 Use the definition (1) of the matrix exponential to prove the basic properties listed in(e) the variance of Y 4 Let Y be a random variable having mean µ and suppose that E(Y −µ)4 ≤ 2 Use this information to determine a good upper bound to P(Y −µ ≥ 10) 5 Let U and V be independent random variables, each uniformly distributed on 0,1 Set X = U V and Y = U − V Determine whether or not X and Y are




2 3 Tangent Plane To A Surface Mathematics Libretexts




X Intercept Of A Line Video Khan Academy
A y″ b y′ c y = 0 Where a, b, and c are constants, a ≠ 0 A very simple instance of such type of equations is y″ − y = 0 The equation's solution is any function satisfying the equality y″ = y Obviously y1 = e t is a solution, and so is any constant multiple of it, C1 e t Not as obvious, but still easy to see, is that y 2If X and Y are independent, then E(es(XY )) = E(esXesY) = E(esX)E(esY), and we conclude that the mgf of an independent sum is the product of the individual mgf's Sometimes to stress the particular rv X, we write MTheorem 36 Let F be any partition of the set S Define a relation on S by x R y iff there is a set in F which contains both x and y Then R is an equivalence relation and the equivalence classes of R are the sets of F Pf Since F is a partition, for each x in S there is one (and only one) set of F which contains x



Regression Basics
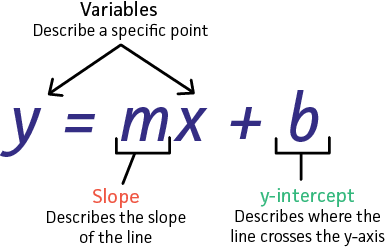



Lines Y Mx B And The Regression Formula Mpa 630 001 Statistical Analysis
Here is how you do it Given, two points, #(x_1,y_1)# and #(x_2,y_2)# and #y= ae^(bx)#X n EXjBnP(Bn) Now suppose that X and Y are discrete RV's If y is in the range of Y then Y = y is a event with nonzero probability, so we can use it as the B in the above So f(xjY = y) is de ned We can change the notation to make it look like the continuous case and writeNCSS Statistical Software NCSScom Curve Fitting – General 3515 © NCSS, LLC All Rights Reserved 7 PolyRatio(4,4) Y=(ABXCX^2DX^3EX^4) / (1FXGX^2HX^3IX^4)
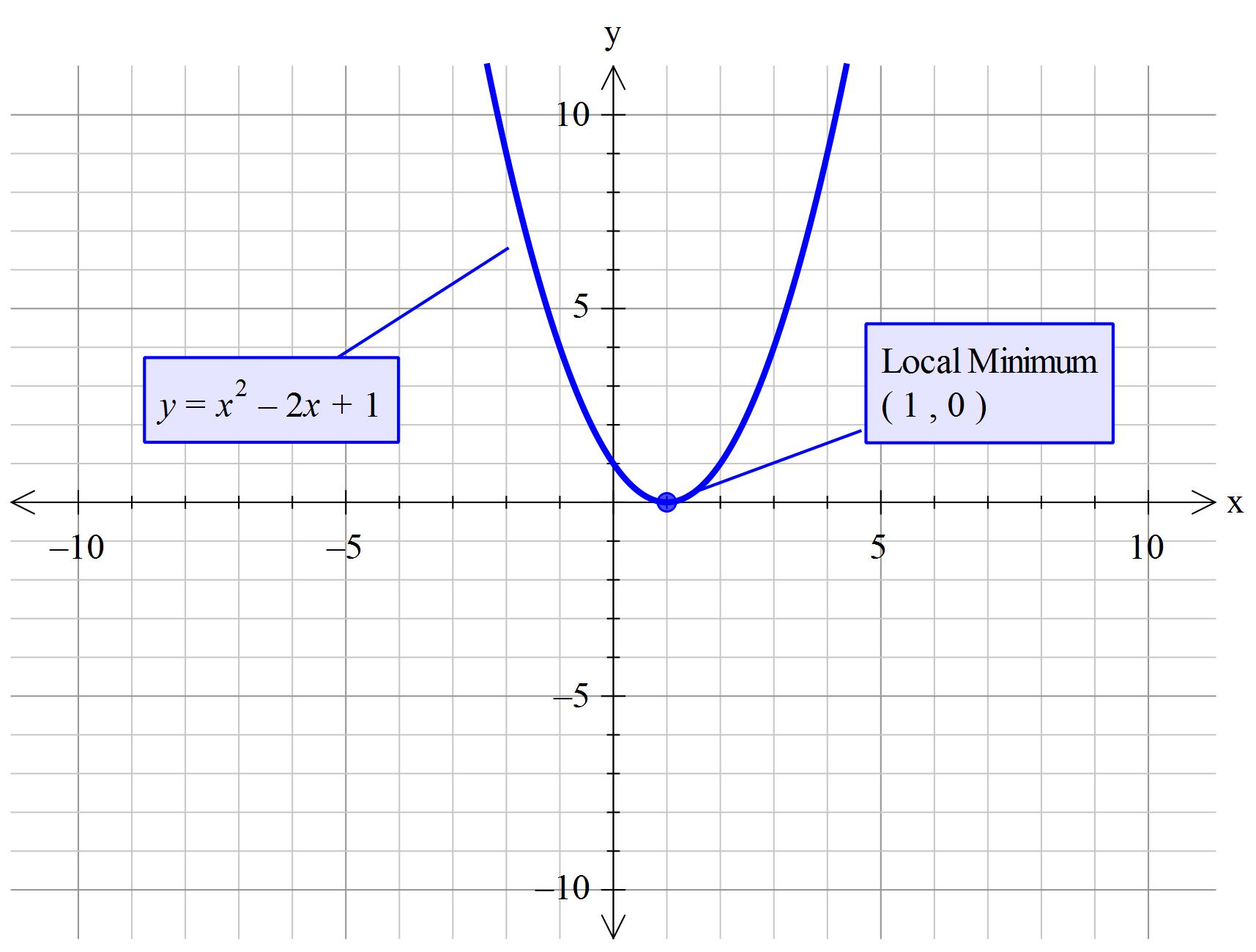



What Is The Vertex Of Y X 2 2x 1 Socratic
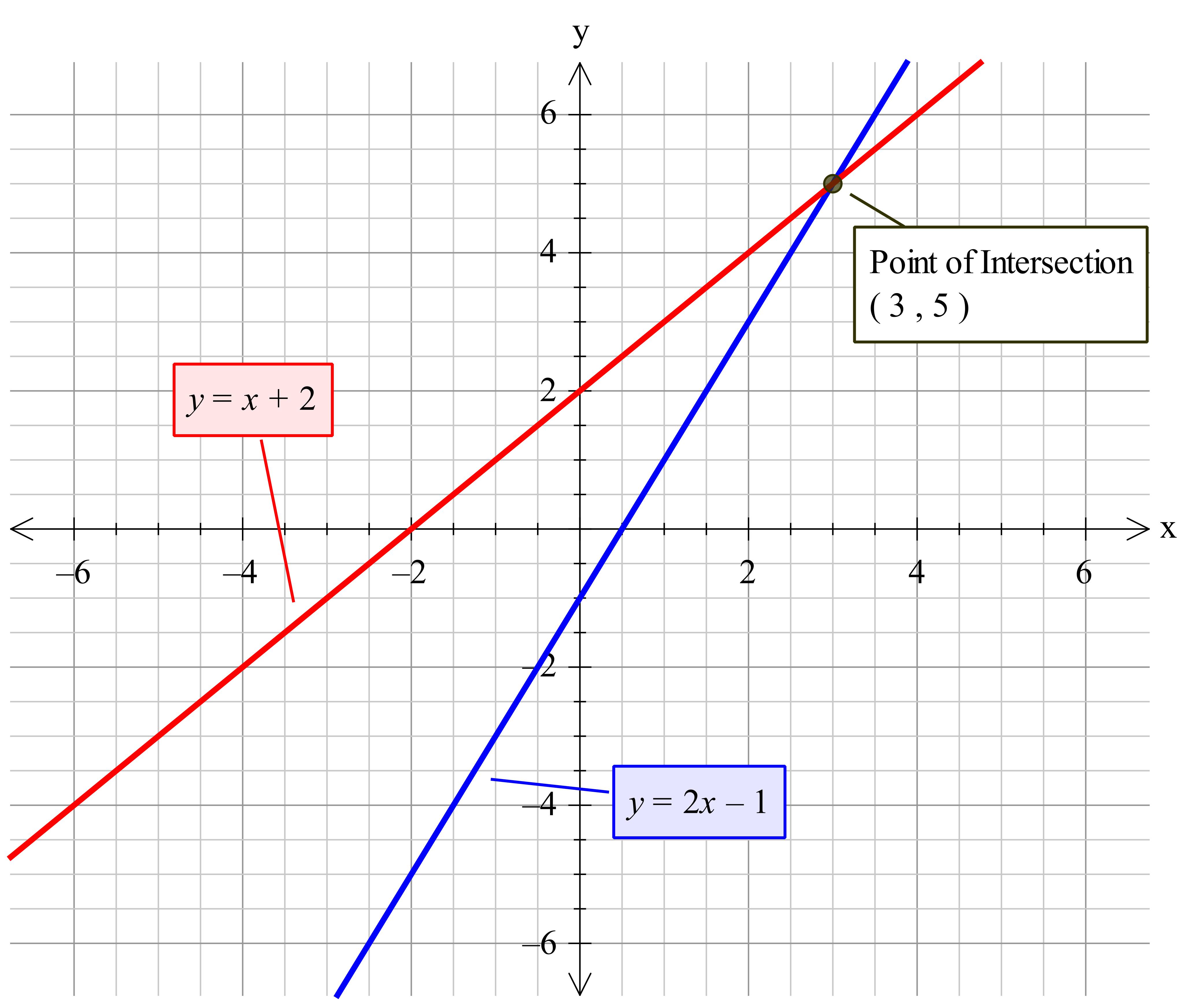



How Do You Solve Y 2x 1 And Y X 2 Socratic
It means the slope is the same as the function value (the y value) for all points on the graph Example Let's take the example when x = 2 At this point, the y value is e 2 ≈ 739 Since the derivative of e x is e x, then the slope of the tangent line at x = 2 is also e 2 ≈ 739 x = 2 \displaystyle {x}= {2} x= 2In this setting, e 0 = 1, and e x is invertible with inverse e −x for any x in B If xy = yx, then e x y = e x e y, but this identity can fail for noncommuting x and y Some alternative definitions lead to the same function For instance, e x can be defined as → ()STAT 400 Joint Probability Distributions Fall 17 1 Let X and Y have the joint pdf f X, Y (x, y) = C x 2 y 3, 0 < x < 1, 0 < y < x, zero elsewhere a) What must the value of C be so that f X, Y (x, y) is a valid joint pdf?b) Find P (X Y < 1)c) Let 0 < a < 1 Find P (Y < a X) d) Let a > 1 Find P (Y < a X)e) Let 0 < a < 1 Find P (X Y < a)



Y A F K X D C




Shimano Junction B Ew Jc130 E Tube Di2 Y Split Cable 3 Connectors 550mm 50mm 550mm
= λ X∞ k=1 λ λk−1 (k −1)!Integrate 1/(cos(x)2) from 0 to 2pi;For b = 1, 2, 3, 4 Describe the graphical significance of b (b) Find the coordinates of the critical point of
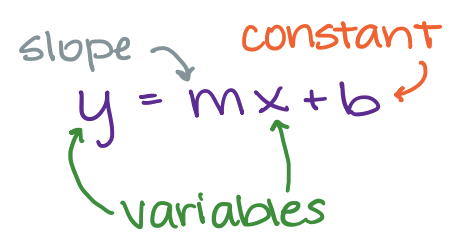



Find Slope And Y Intercept From Equation Process Expii




Show That Operatorname Cov X A By B Operatorname Cov X Y Mathematics Stack Exchange
#e^b= 3/8# #b = ln(3/8)# The final equation is #y = 8e^(ln(3/8)x)# Often, the same problem is asked where the x coordinate of one of the points is not 0 When this happens, you must find the value of #b# before you find the value of #a#;EB(u)B(v) = min(u,v), we have Cov(Y(s),Y(t)) = EY(s)Y(t) −EY(s)EY(t) = EY(s)Y(t) = EsB(1/s)tB(1/t) = stEB(1/s)B(1/t) = stmin(1 s, 1 t) =min(t,s) (c) Clearly Y(t)=tB(1/t) has a continuous sample path, as B has a continuous sample path Second, as shown in part (a) the Y(t) has normal distribution with mean 0 and variance tThe fact that some of the coeffi cients are functions of x should not slow us down Applying the quadratic formula we get y = ex ± (−ex)2 − 4 1 (−ex) 2 1 ex± √ 2 4 y = 2 Our original equation is valid only for y > 0, and √ e2x 4ex > √ e2x = e
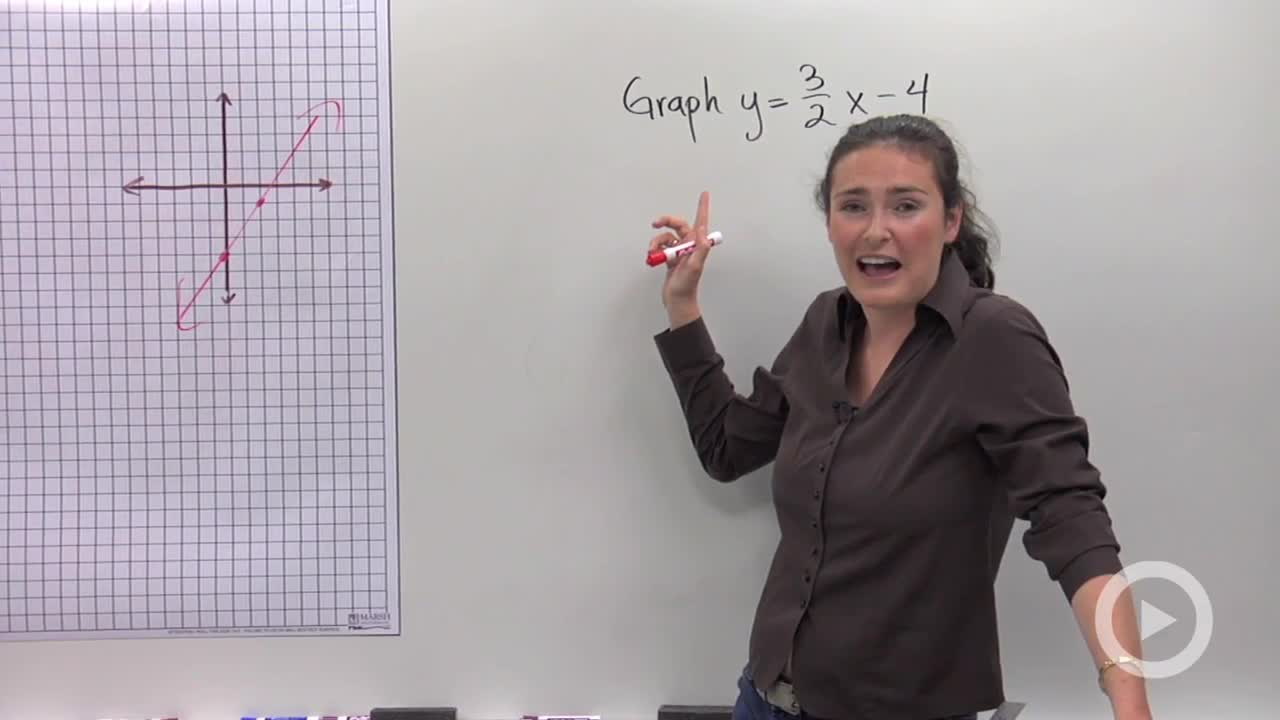



How To Graph A Line Using Y Mx B Problem 1 Algebra Video By Brightstorm



2
Of x and t (and not y or z), so all y and zderivatives are zero yyzz0 EBEB yz y z EB00 Recall, in a chargefree medium, xxyyzz00 EBEBEB xy z x y z that is, xx00 EB xx We find and The component of the wave pointing parallel to the propagation direction does not vary along that direction Only E y and E z can vary with xD(x,y) ≥ d(y,zx)−d(x,zx) ≥ d(y,zy)−d(x,zx) = d(x,E) −d(y,E) Besides, in the case that d(x,E) ≥ d(y,E), we can get d(x,y) ≥ d(y,E) − d(x,E) So we can conclude that d(x,E) −d(y,E) ≤ d(x,y) ∀x0 ∈ X,∀ε > 0, just choose δ = ε 2, then ∀x ∈ B(x0,δ), we have d(x,E) − d(x0,E) ≤ d(xIe a way to measure distances between elements of XA distanceor metric is a function d X×X →R such that if we take two elements x,y∈Xthe number d(x,y) gives us the distance
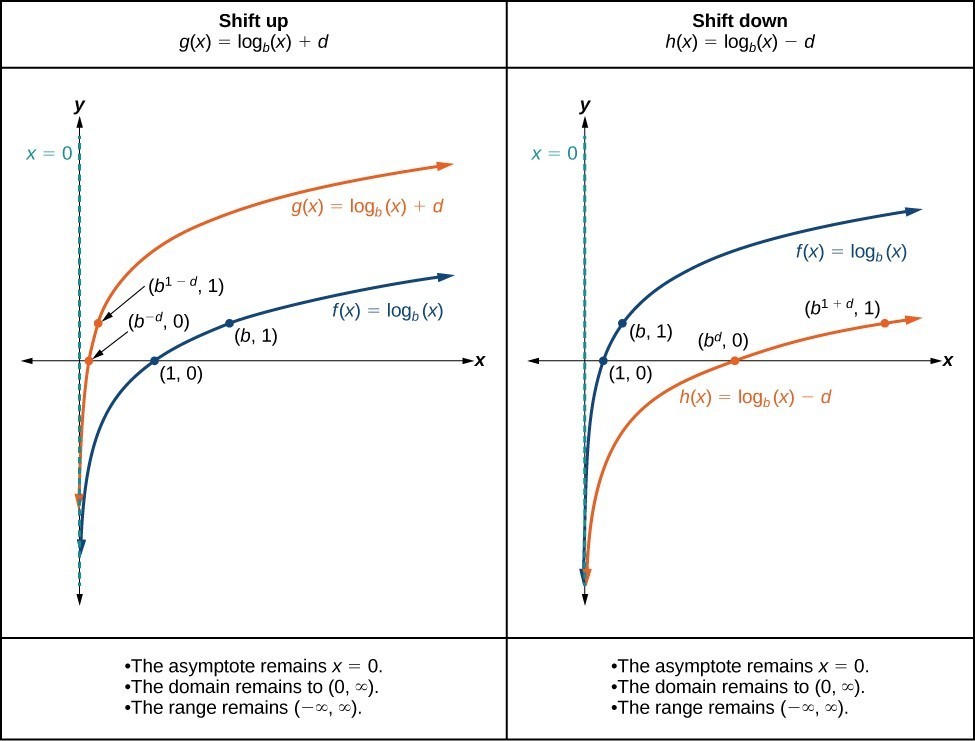



Graphing Transformations Of Logarithmic Functions College Algebra
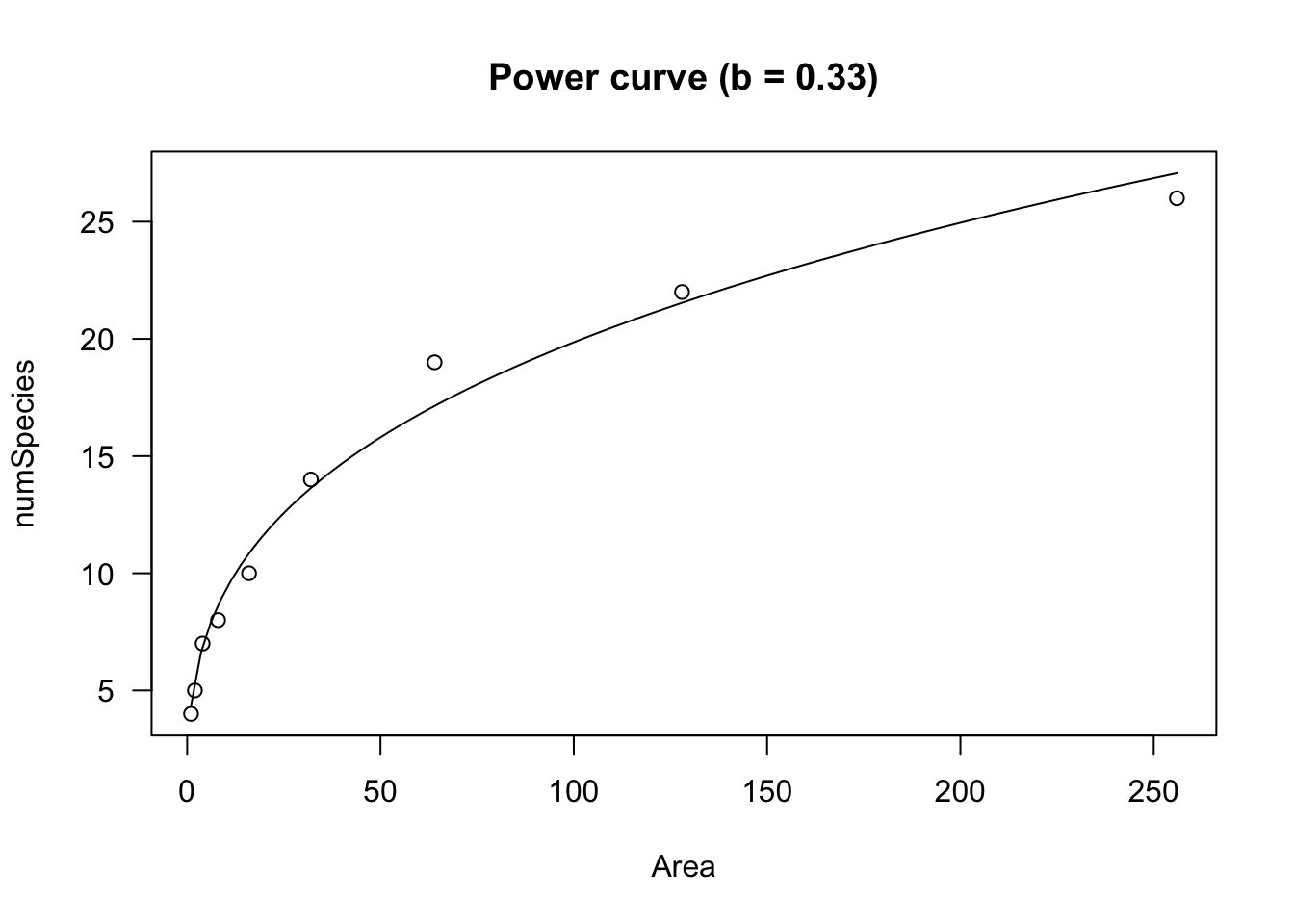



Some Useful Equations For Nonlinear Regression In R
View more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn




Show That Operatorname Cov X A By B Operatorname Cov X Y Mathematics Stack Exchange




3 Ways To Find The Y Intercept Wikihow




Btl B Y Wing Star Wars X Wing Fantasy Flight Games Ffgswz48



Exploration Of Parabolas
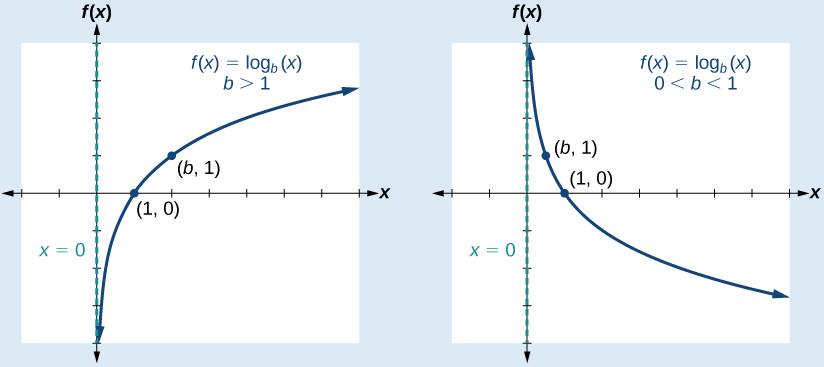



Graphs Of Logarithmic Functions Algebra And Trigonometry
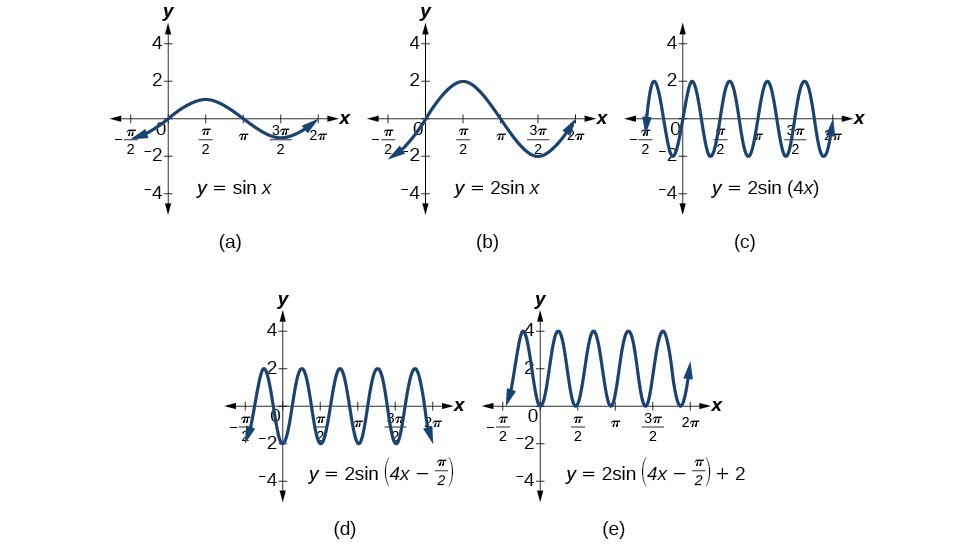



Modeling With Trigonometric Equations Precalculus Ii
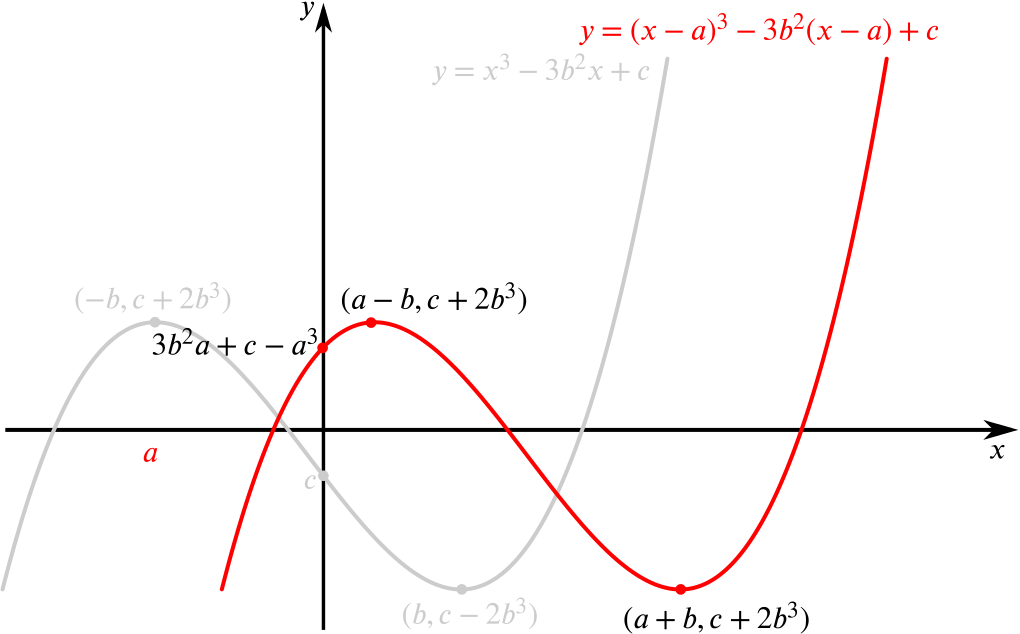



Solution When Does This Cubic Equation Have Distinct Real Positive Solutions Calculus Meets Functions Underground Mathematics




Mathematics For Machine Learning Linear Regression Least Square Regression By Daksh Gupta Towards Data Science




How To Graph Y Sqrt X Video Lesson Transcript Study Com




Q29 Answers Paper 1 June 18 Aqa Gcse Maths Higher Elevise




Prove That X Y Leq X Y Mathematics Stack Exchange
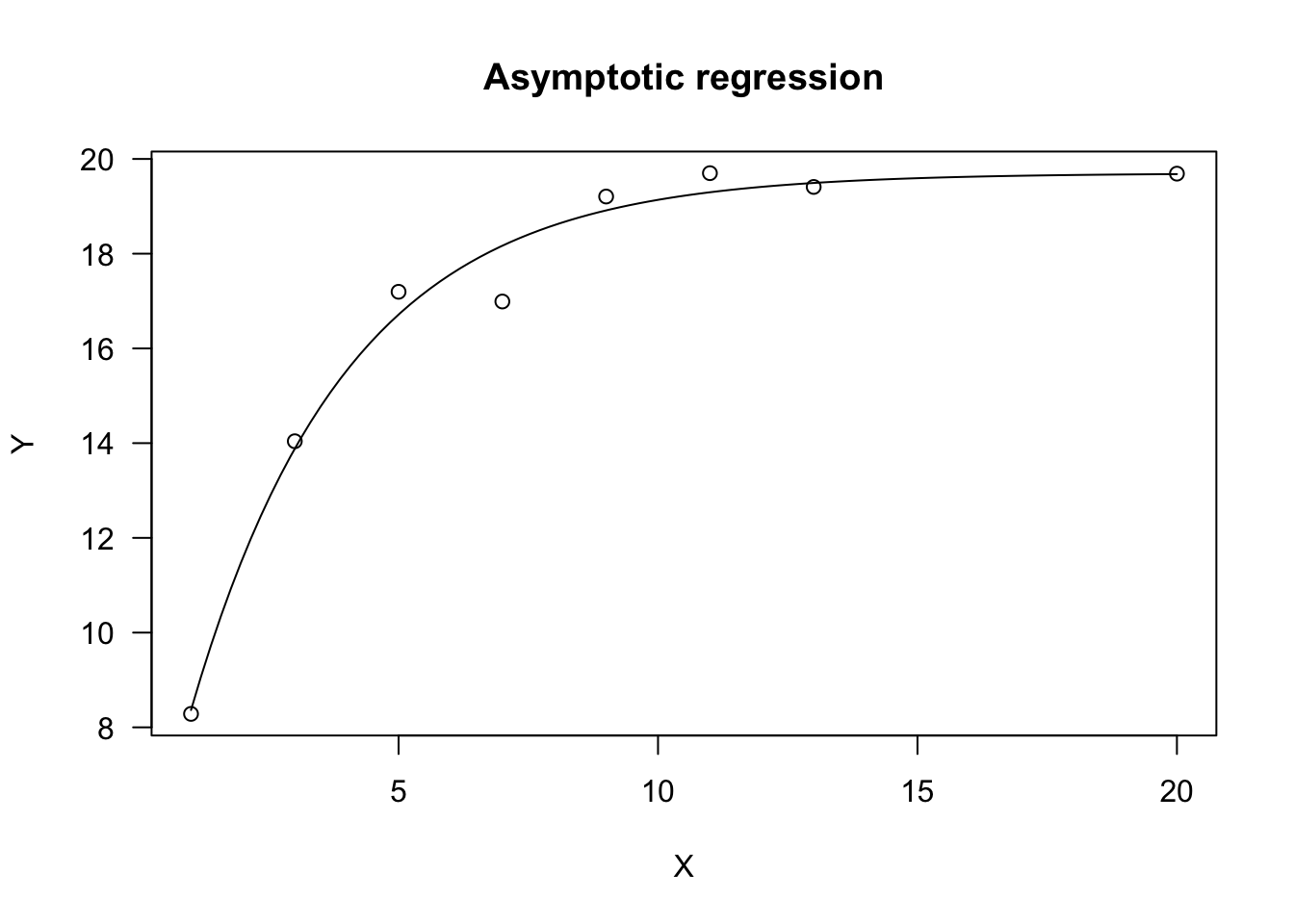



Some Useful Equations For Nonlinear Regression In R
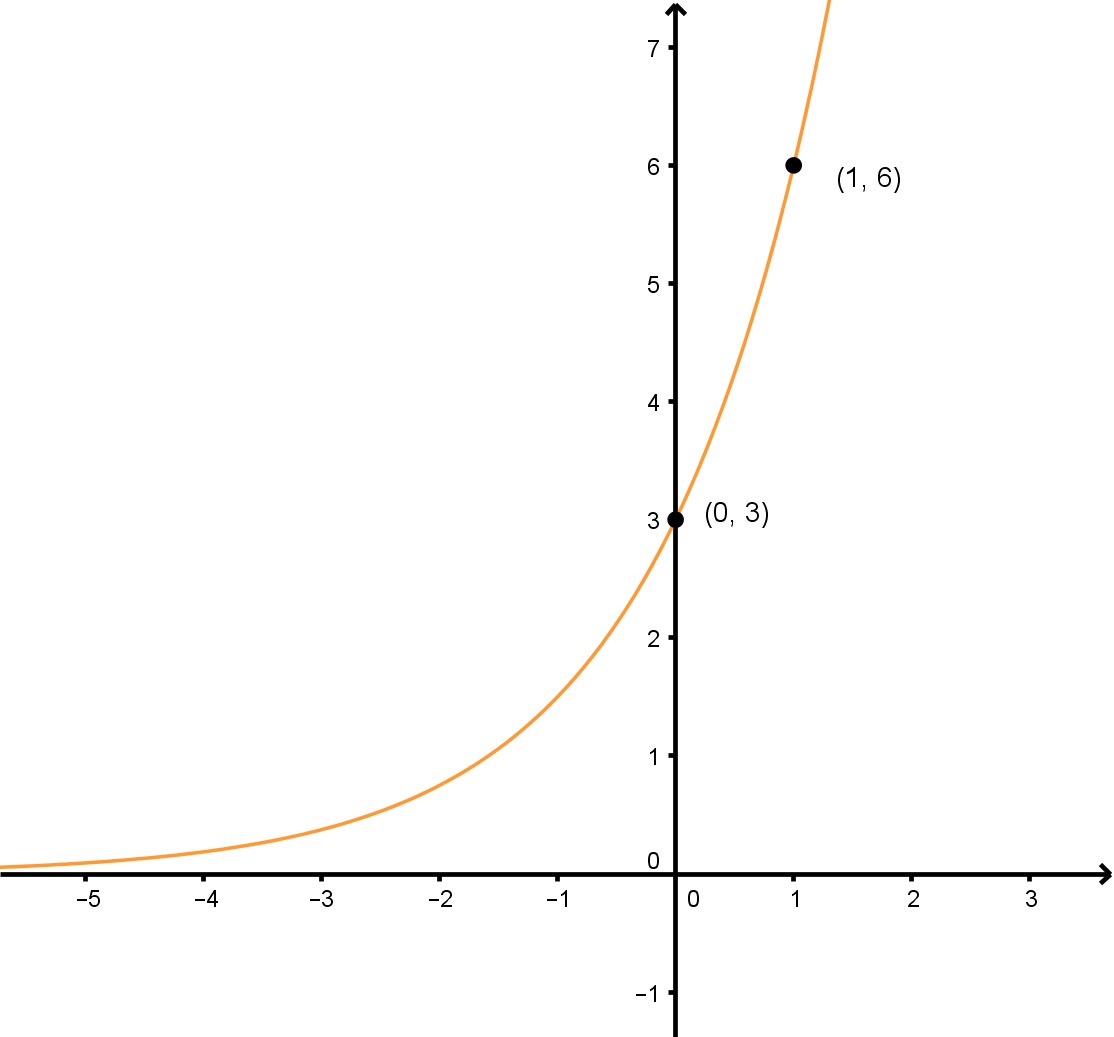



How To Find Equations For Exponential Functions Studypug
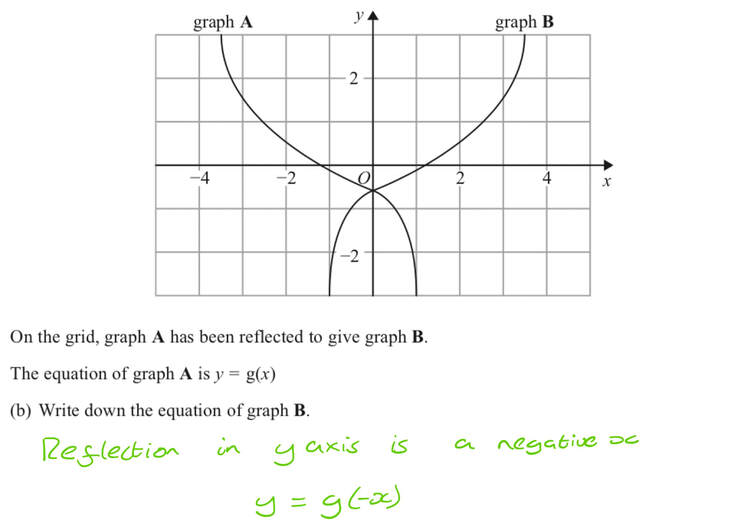



Q18 Answers Paper 1 November 18 Edexcel Gcse Maths Higher Elevise




Reflection Over The Y X Line Youtube
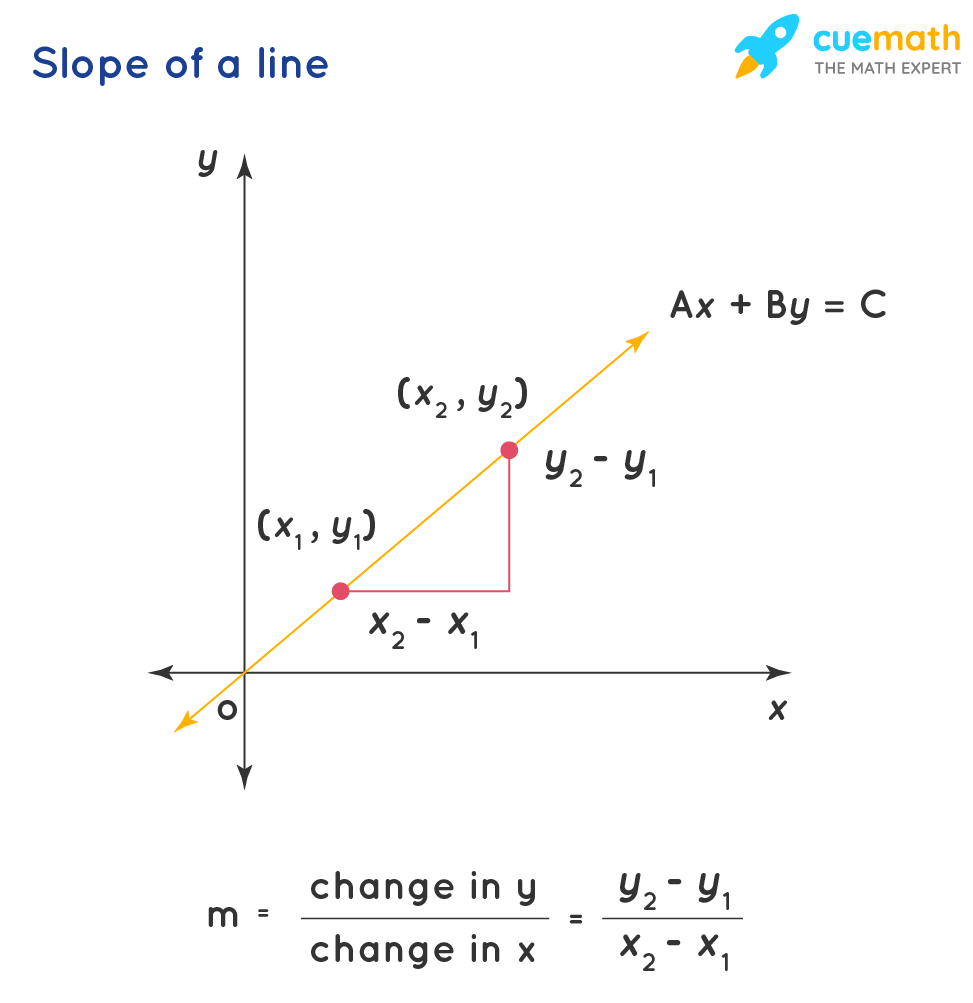



Y Mx B What Is Meaning Of Y Mx B How To Find Slope And Y Intercept
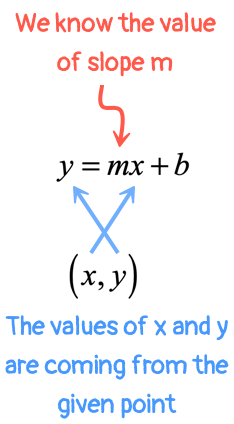



Slope Intercept Form Of A Straight Line Y Mx B Chilimath



1
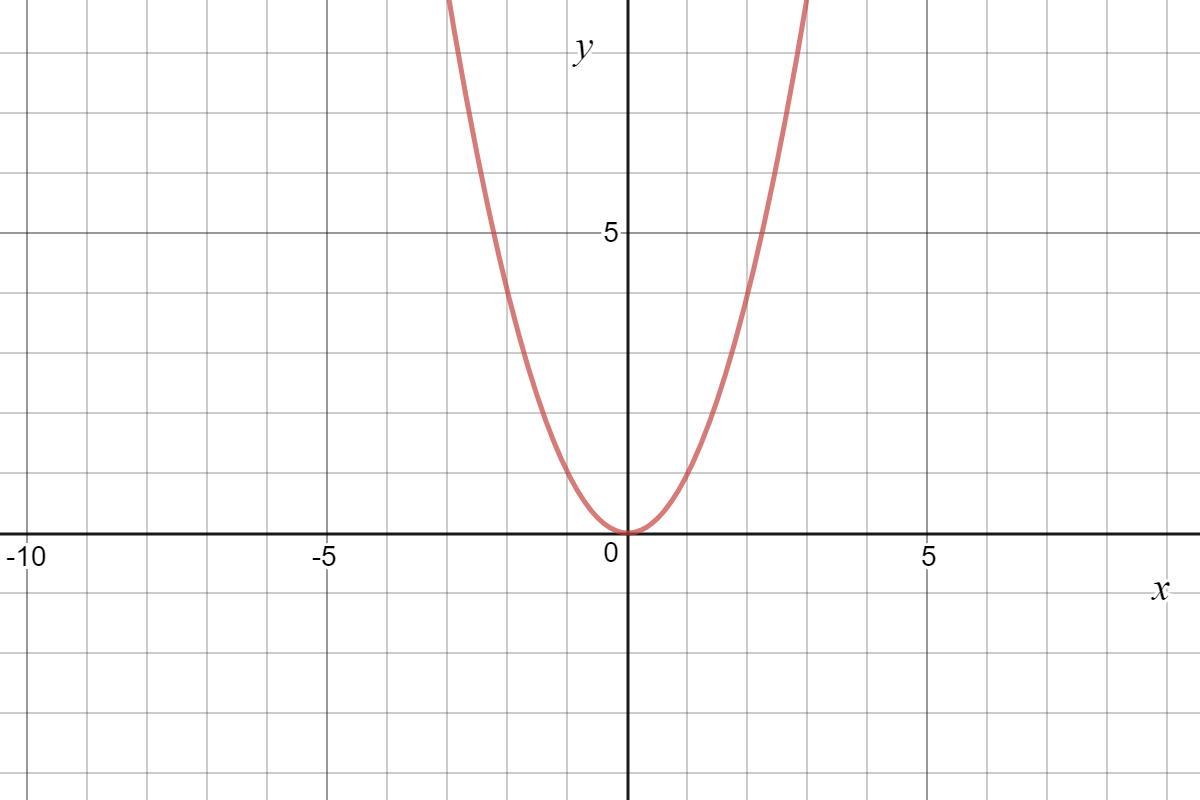



Quadratic Graph Example Y Ax C Expii




Prove That The Line X A Y B 1 And X B Y A 1 Are Perpendicular To Each Other




2 5 Quiz 14 Answers Linear Graphs Aqa Gcse Maths Higher Elevise



1




Fantasy Flight Games Ffgswz48 Star Wars X 2nd Edition Btl B Y Wing Expansion Pack Mixed Colours Amazon Co Uk Toys Games



Linear Intercepts Maths First Institute Of Fundamental Sciences Massey University



1
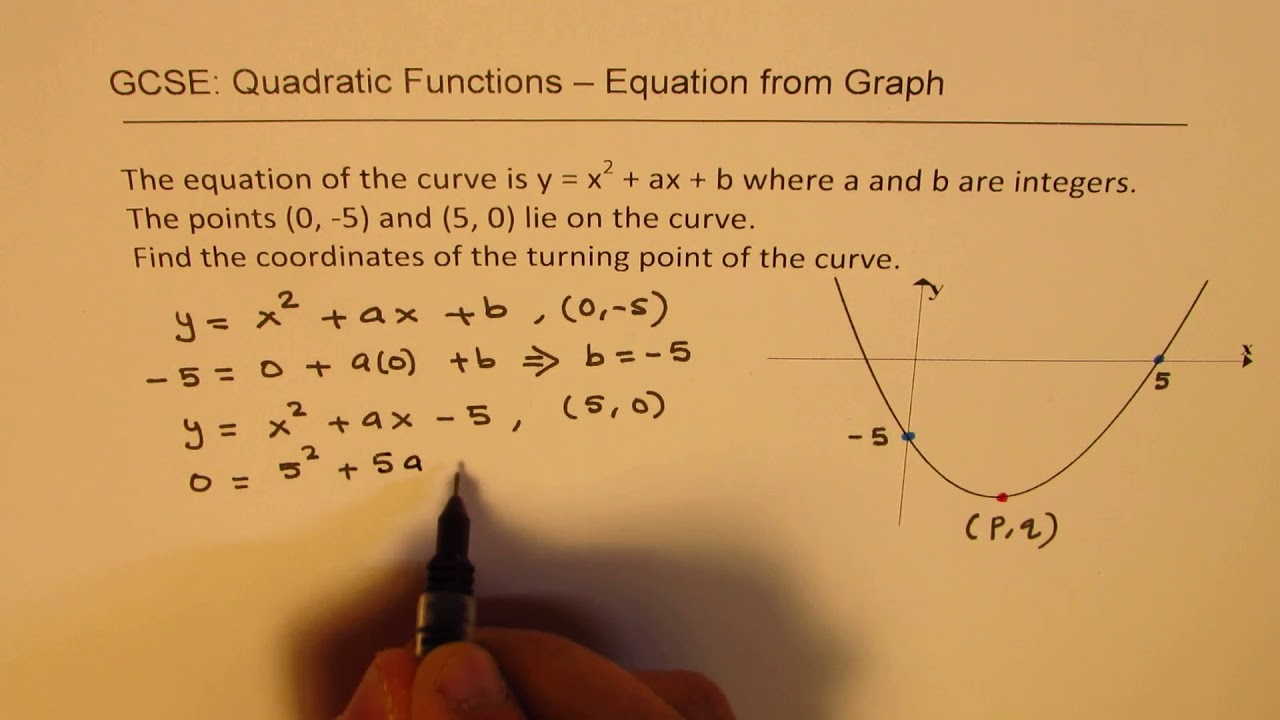



Gcse X 2 Ax B Find Turning Point When Given Intercepts 5 0 And 0 5 Youtube




Solved X And Y Are Random Variables A Show That Chegg Com
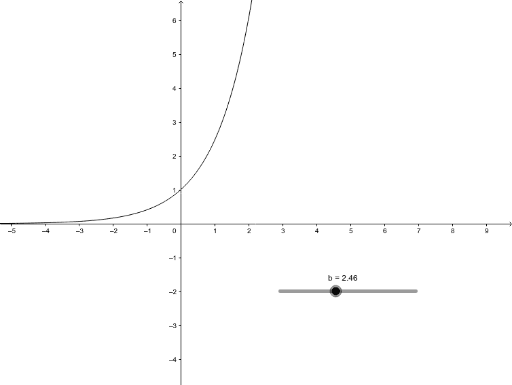



Graph Of Y B X Geogebra



Plot A Function Y F X In Python W Matplotlib




How To Find The Equation Of A Line 8 Steps With Pictures
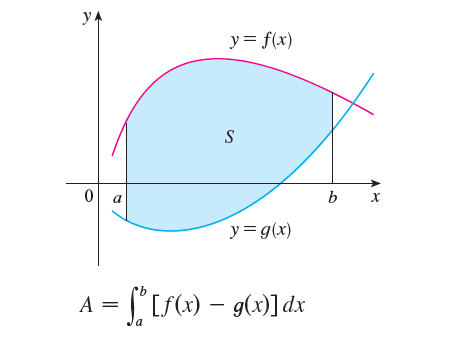



Find Area Between Two Curves Examples
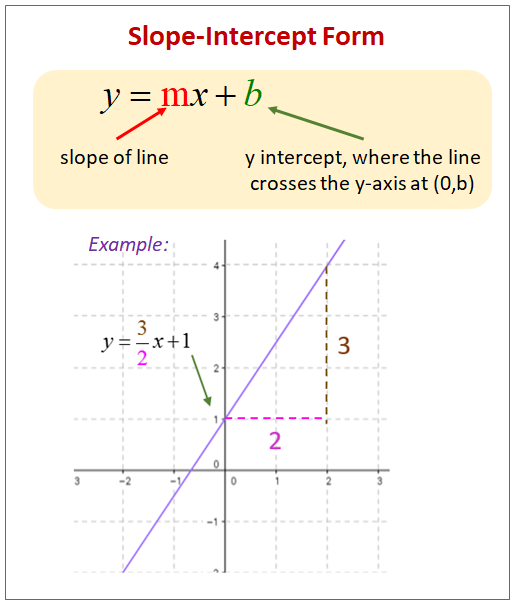



Equation Of A Line Video Lessons Examples Solutions



Logarithmic And Exponential Graphs



Quadratics




Beta Function Wikipedia




Review Of Probability And Statistics I E Things




Solved As A Hint We Can Prove Cov Ax B Cy Ac Cov X Y Chegg Com
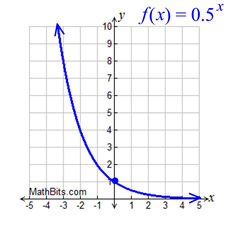



Exponential Functions Mathbitsnotebook A1 Ccss Math



In The Equation Y Ab X What Does Each Symbol Mean Which Is The Initial Amount And Which Is The Growth Factor Quora
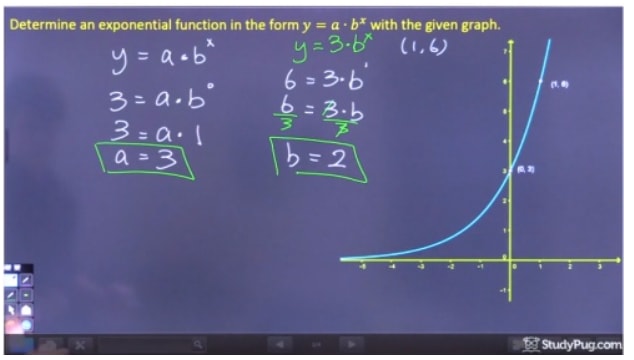



How To Find Equations For Exponential Functions Studypug



Equation Of A Line The Derivation Of Y Mx B




Interpret The Graph Of Frac Ax B Cx D As A Transformation Of Y Frac 1 X Mathematics Stack Exchange




Excel Formula Count Cells Equal To Either X Or Y Exceljet




Ex 9 3 5 Form Differential Equation Y Ex A Cos X B Sin X
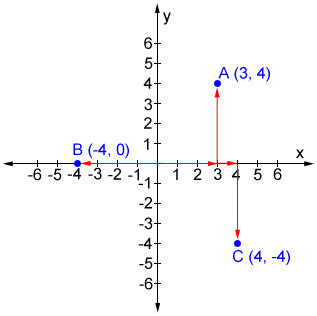



X And Y Axis
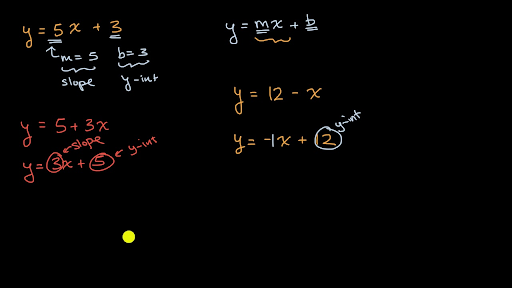



Slope And Y Intercept From Equation Video Khan Academy




Proof E X E Y E X Y 77neurons Project Perelman A Mathematics Project By Jad Nohra And Tom Lahore



1




How To Graph The Line Y X Youtube



Handbook For Spoken Mathematics



How Do You Sketch The Graph Of Y X 2 2x And Describe The Transformation Socratic
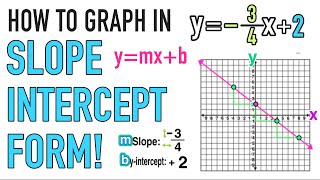



How To Graph Lines In Slope Intercept Form Y Mx B Youtube




An Example Of A Hyperbola Of Equation X 2 A 2 Y 2 B 2 1 With Download Scientific Diagram




Conditionals And Loops
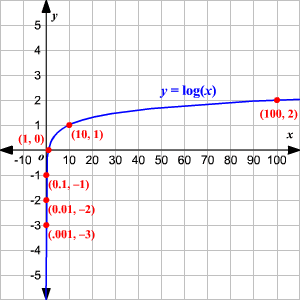



Graphing Logarithmic Functions




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Definition Of A Logarithmic Function For X 0 And B 0 B 1 Y Log B X Is Equivalent To B Y X The Function F X Log B X Is The Logarithmic Function Ppt Download
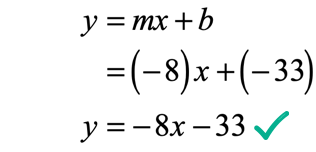



Slope Intercept Form Of A Straight Line Y Mx B Chilimath




Example 33 Find Dy Dx If Y X X Y X X A B Teachoo
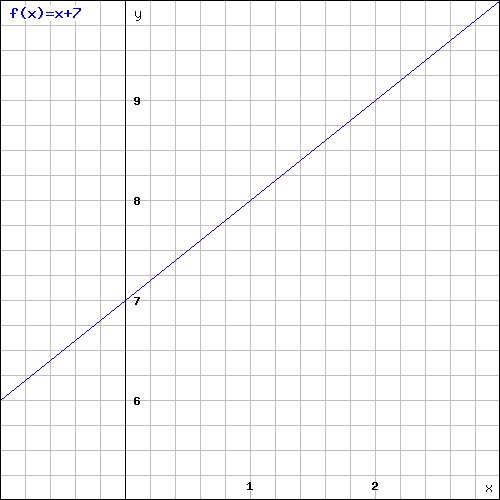



Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet



Emat6680 Gif Assignment 1 Exploring Graphs Of Common Logs And Natural Logs By Jenny Johnson The Purpose Of This Exploration Is To Examine The Graphs Of Common Logarithms Y A Log Bx And Natural Logarithms Y A Ln Bx What Are The
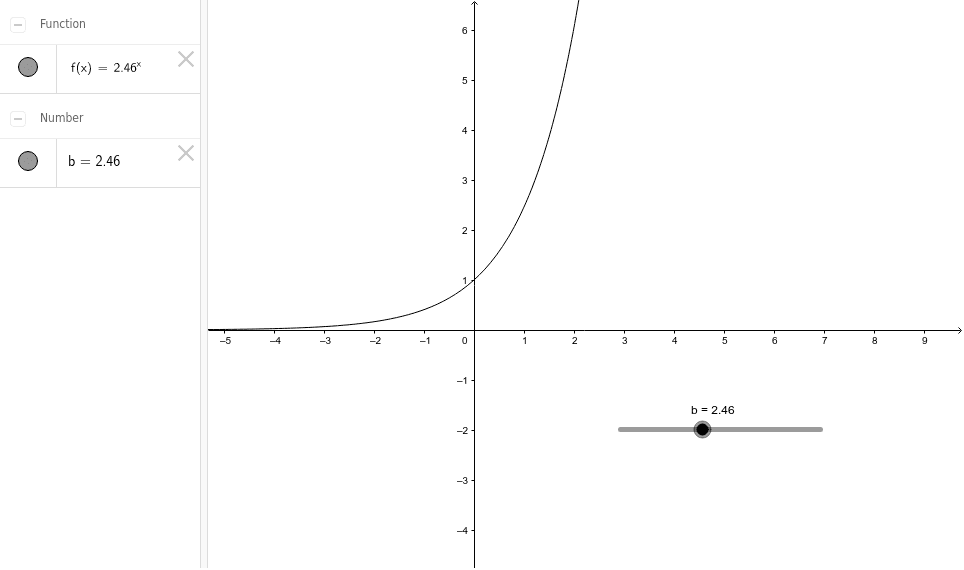



Graph Of Y B X Geogebra




Inline Usb 3 0 Y Cable 2 X Micro B To B 2 M Black Inline




0 1 X
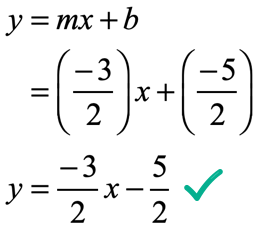



Slope Intercept Form Of A Straight Line Y Mx B Chilimath
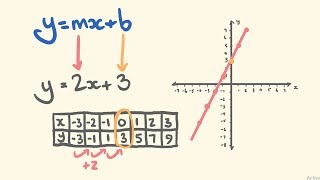



Graphing Linear Equations Using Y Mx B Slope Intercept Youtube



Exponetials And Growth Functions
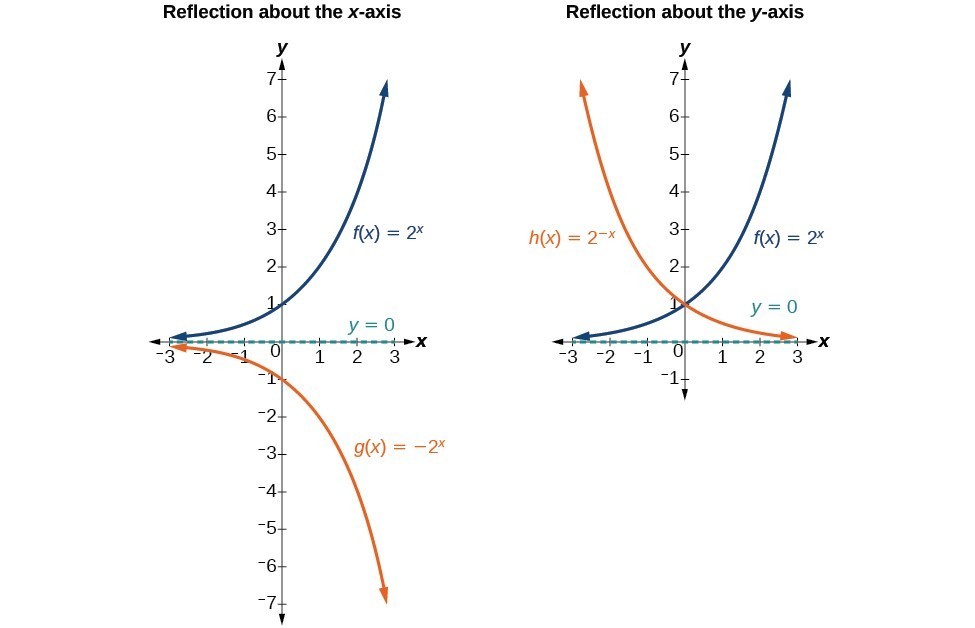



Stretching Compressing Or Reflecting An Exponential Function College Algebra



Regression Basics




Equation Of A Straight Line
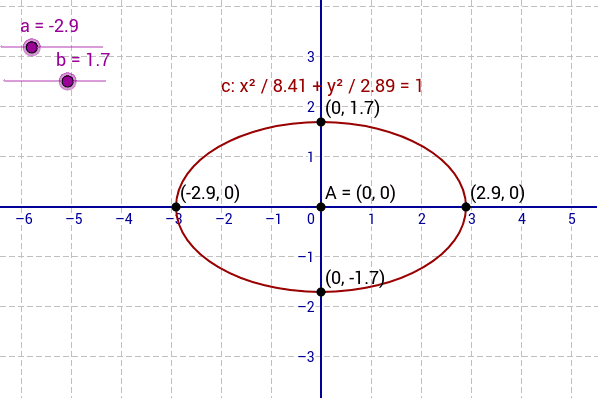



Equation Of An Ellipse X A 2 Y B 2 1 Geogebra




Definition Of A Logarithmic Function For X 0 And B 0 B 1 Y Log B X Is Equivalent To B Y X The Function F X Log B X Is The Logarithmic Function Ppt Download




Ex 2 1 6 If A X B A X A Y B X B Y Find A B



Straight Line Graphs Of The Form Y A X B Y X Matching Pairs
コメント
コメントを投稿